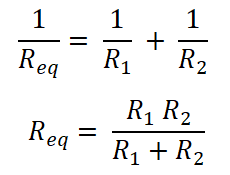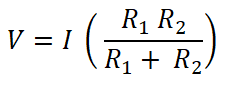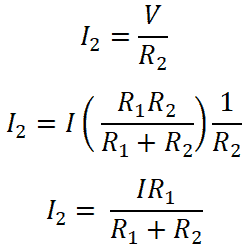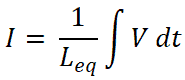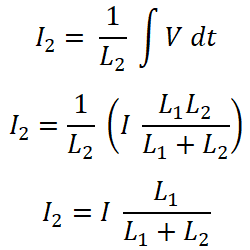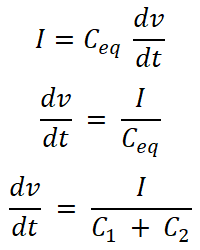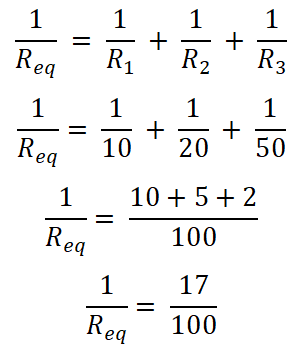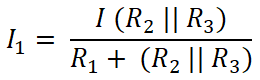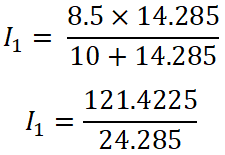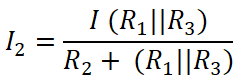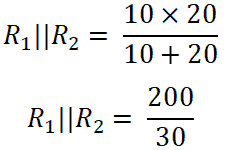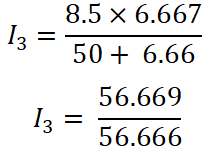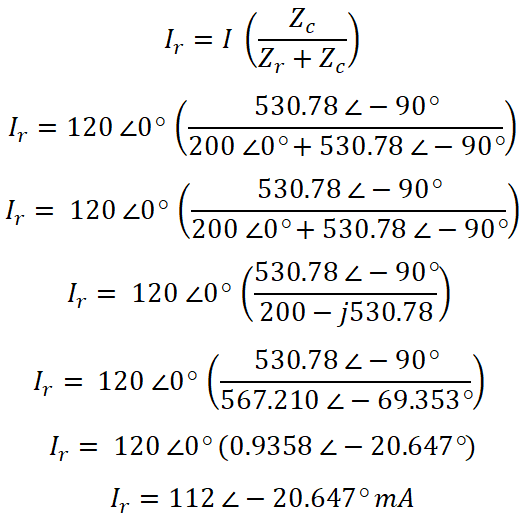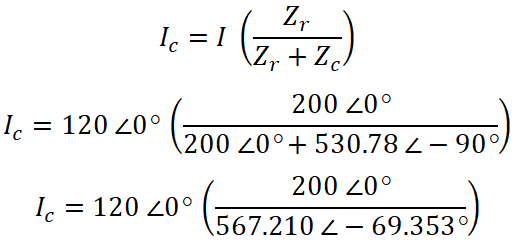Current Divider Rule (CDR) – Solved Examples for AC and DC Circuits

Current Division “CDR” for for Resistive, Inductive and Capacitive Circuits

What is Current Divider Rule (CDR)?

When a number of elements are connected in parallel, the current divides into a number of parallel paths. And the voltage is the same for all elements which are equal to the source voltage.

In other words, when the current passes through more than one parallel path (the voltage divider rule “VDR” or voltage division is used to calculate the voltage in the series circuits), the current divide in each path. The value of current passes through a particular branch depends on the impedance of that branch.

The current divider rule or current division rule is the most important formula that is widely used to solve circuits. We can find the current that passes through each branch if we know the impedance of each branch and the total current.

The current always flows through the least impedance. So, the current has an inverse relationship with impedance. According to ohm’s law, the current that enters the node will be split between them in inverse proportion to the impedance.

It means that the smaller value impedance has a larger current as the current chose the least resistance path. And the larger value resistance has the least current.

According to the circuit elements, the current divider rule may describe resistors, inductors, and capacitors.

Related Posts:

• Current Divider Rule Calculator – CDR Formula & Calculations
  
• Voltage & Current Divider Rules (VDR & CDR) Equations

Current Divider Rule for Resistive Circuits

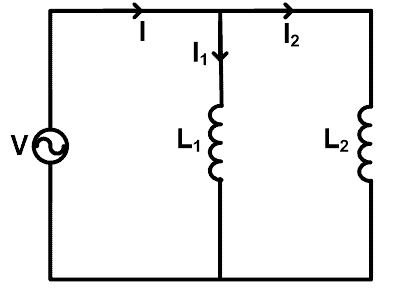
To understand the resistive current divider rule, let’s take a circuit in which the resistors are connected in parallel. The circuit diagram is shown in the figure below.

In this example, a DC source supply to all resisters. The voltage of resisters is the same as the source voltage. But due to parallel connection, the current divides into different paths. The current divides at each node and the value of current depend on the resistance.

We can directly find the value of current passing through each resistor with the help of the current divider rule.

In this example, the main current supplied by the source is I. And it divides into two resistors R₁ and R₂. The current passes through the resistor R₁ is I₁ and the current passes through the resistor R₂ is I₂.

As the resistors are connected in parallel. So, the equivalent resistance is R_eq.

Now, according to Ohm’s law;

V = I R_eq

Both resisters are connected in parallel with a DC source. Therefore, the voltage across the resistor is the same as the source voltage. And the current that passes through the resistor R₁ is I₁.

So, for resister R₁;

Similarly, for resister R₂;

So, these equation shows a current divider rule for resistance connected in parallel. From these equations, we can say that the current that passes through resister is equal to the ratio of multiplication of total current and opposite resistance with the total resistance.

Related Posts:

• Thevenin’s Theorem. Step by Step Guide with Solved Example
• Norton’s Theorem. Step by Step Guide with Solved Example

Current Divider Rule for Inductive Circuits

When inductors are connected in parallel, we can apply the current divider rule to find the current that passes through each inductor. To understand the current divider rule, we take a circuit in which the inductors are connected in parallel as shown in the figure below.

Here, two inductors (L₁ and L₂) are connected in parallel with a source voltage V. Total current passes through the source is I ampere. The current passes through the inductor L₁ is I₁ and the current passes through the inductor L₂ is I₂.

Now, we need to find the equations for current I₁ and I₂. For that, we will find the equivalent inductance L_eq;

We know that the total current passes through the circuit are I and it is equating as;

So,

Now, for inductor L₁, current passes through this inductor is I₁;

For inductor L₂;

The current divider rule for the inductor is the same as the current divider rule for the resistors.

Related Posts:

• Superposition Theorem – Circuit Analysis with Solved Example
• Maximum Power Transfer Theorem for AC & DC Circuits

Current Divider Rule for Capacitive Circuits

When the capacitors are connected in parallel, we can find the current passes through each capacitor by using the current divider rule. To understand the current divider rule for the capacitor, we take an example in which the capacitors are connected in parallel as shown in the figure below.

Here, two capacitors (C₁ and C₂) are connected in parallel with a voltage source V. The current passes through the capacitor C₁ is I_1, and the current passes through the capacitor C₂ is I₂. The total current supplied through the source is I.

Now, we need to find the equations for current I₁ and I₂. For that, we will find the equivalent capacitance C_eq;

C_eq = C₁ + C₂

We know the equation for the current that passes through the capacitor. And the equation for the total current supplied by the source is;

For capacitor C₁, the current that passes through this capacitor is I₁;

For Capacitor C₂;

The current divider rule for the capacitor is slightly different from the current divider rule for the inductor and resistor.

In the capacitor current divider rule, the current passes through a capacitor is a ratio of the total current multiplied by that capacitor to the total capacitance.

Related Posts:

• Millman’s Theorem – Analyzing AC & DC Circuits – Examples
• Tellegen’s Theorem – Solved Examples & MATLAB Simulation

Solved Examples for AC and DC Circuits using CDR

Current Diver Rule for DC Circuit

Example:1

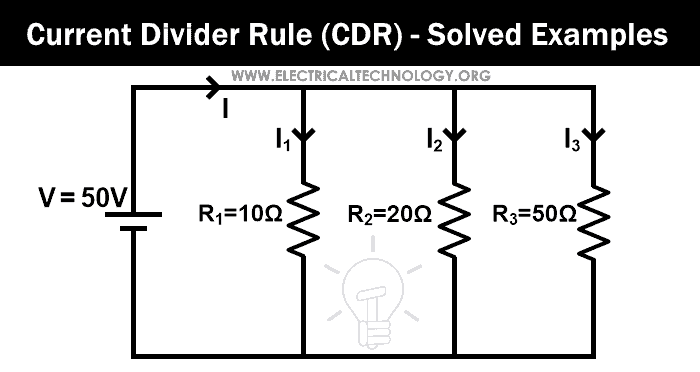
Find the current passes through each resistor by the current divider rule for the given network.

In this example, three resistors are connected in parallel. First, we find the equivalent resistance.

R_eq = 100/17

R_eq = 5.882 Ω

The total current supplied by the source is I. So, according to ohm’s law;

V = I R_eq

50V = I (5.882Ω)

I = 50V / 5.882Ω

I = 8.5 A

Now, we apply the current divider rule to the first resister (10 Ω), and the current passes through this resister is I₁;

Here R₂ and R₃ are connected in parallel. So, we need to find the equivalent resistance between R₂ and R₃.

(R₂ || R₃ ) = 14.285 Ω

I₁ = 4.9999 ≈ 5 A

Similarly, we apply the current divider rule to the Second resistor (20 Ω), and the current that passes through this resister is I₂;

Here,

(R₁ || R₃ ) = 8.33 Ω

I₂ = 2.499 ≈ 2.5 A

Now, we apply the current divider rule to the third resistor (50 Ω), and the current that passes through this resistor is I₃.

Here,

(R₁ || R₂ ) = 6.66 Ω

I₃ = 1.00 A

So, the summation of all three currents will be;

I₁ + I₂ + I₃ = 5 + 2.5 + 1 = 8.5 A

And this current is the same as the total current supplied by the source.

Related Posts:

• Voltage Divider Rule (VDR) – Solved Examples for R, L and C Circuits
• Voltage Divider “VDR” Calculator, Examples & Applications

Current Diver Rule for AC Circuit

Example-2

Consider an AC circuit having a resistor and capacitor connected in parallel as shown in the figure below. Find the current passes through the resistor and capacitor using the current divider rule. Consider 60 Hz frequency.

Z_R = 200 Ω = 200∠0°Ω

Z_C = 1/(2 πfC) = 1/(2 π 60(5×10⁶) )

Z_C = 10⁶ / (600 π)

Z_C = 530.78 ∠-90° Ω

Now, according to the current divider rule, the equation of current passes through the resistor is;

Now, similarly, we can find the current passes through the capacitor. According to the current divider rule, the equation of current passes through the capacitor is;

I_C = 120 ∠0° (0.3526 ∠ 69.353°)

I_C = 42.31 ∠ 69.353°

If you want to prove this answer, you can add both currents. And the value of this current is the same as the source current.

Related Electric Circuit Analysis Tutorials:

• Compensation Theorem – Proof, Explanation and Solved Examples
• Substitution Theorem – Step by Step Guide with Solved Example
• SUPERNODE Circuit Analysis – Step by Step with Solved Example
• SUPERMESH Circuit Analysis – Step by Step with Solved Example
• Kirchhoff’s Current & Voltage Law (KCL & KVL) | Solved Example
• Cramer’s Rule Calculator – 2 and 3 Equations System for Electric Circuits
• Wheatstone Bridge – Circuit, Working, Derivation and Applications
• Electrical and Electronics Engineering Calculators
• 5000+ Electrical and Electronic Engineering Formulas & Equations