Delta Connection (Δ): 3 Phase Power, Voltage & Current Values

Electrical Technology

Three Phase Delta Connection: Line, Phase Current, Voltages & Power in Δ Configuration

Table of Contents

What is Delta Connection (Δ)?

Delta or Mesh Connection (Δ) System is also known as Three Phase Three Wire System (3-Phase 3 Wire) and it is the most preferred system for AC power transmission while for distribution, Star connection is generally used.

In Delta (also denoted by Δ) system of interconnection, the starting ends of the three phases or coils are connected to the finishing ends of the coil. Or the starting end of the first coil is connected to the finishing end of the second coil and so on (for all three coils) and it looks like a closed mesh or circuit as shown in fig (1).

In more clear words, all three coils are connected in series to form a close mesh or circuit. Three wires are taken out from three junctions and the all outgoing currents from junction assumed to be positive.

In Delta connection, the three windings interconnection looks like a short circuit, but this is not true, if the system is balanced, then the value of the algebraic sum of all voltages around the mesh is zero in Delta connection.

When a terminal is open in Δ, then there is no chance of flowing currents with basic frequency around the closed mesh.

Voltage, Current and Power Values in Delta Connection (Δ)

Now we will find the values of Line current, Line Voltage, Phase Current, Phase Voltages and Power in three phase Delta AC system.

Line Voltages (V_L) and Phase Voltages (V_Ph) in Delta Connection

It is seen in fig 2 that there is only one phase winding between two terminals (i.e. there is one phase winding between two wires). Therefore, in Delta Connection, the voltage between (any pair of) two lines is equal to the phase voltage of the phase winding which is connected between two lines.

Since the phase sequence is R → Y → B, therefore, the direction of voltage from R phase towards Y phase is positive (+), and the voltage of R phase is leading by 120°from Y phase voltage. Likewise, the voltage of Y phase is leading by 120° from the phase voltage of B and its direction is positive from Y towards B.

If the line voltage between;

Line 1 and Line 2 = V_RY
Line 2 and Line 3 = V_YB
Line 3 and Line 1 = V_BR

Then, we see that V_RY leads V_YB by 120° and V_YB leads V_BR by 120°.

Let’s suppose,

V_RY = V_YB = V_BR = V_L …………… (Line Voltage)

Then

V_L = V_PH

I.e. in Delta connection, the Line Voltage is equal to the Phase Voltage.

Also read : Three Phase Current Values in a 3-Phase System

Line Currents (I_L) and Phase Currents (I_Ph) in Delta Connection

It will be noted from the below (fig-2) that the total current of each Line is equal to the vector difference between two phase currents in Delta connection flowing through that line. i.e.;

Current in Line 1= I₁ = I_R – I_B
Current in Line 2 =I₂ = I_Y – I_R
Current in Line 3 =I₃ = I_B – I_Y

{Vector Difference}

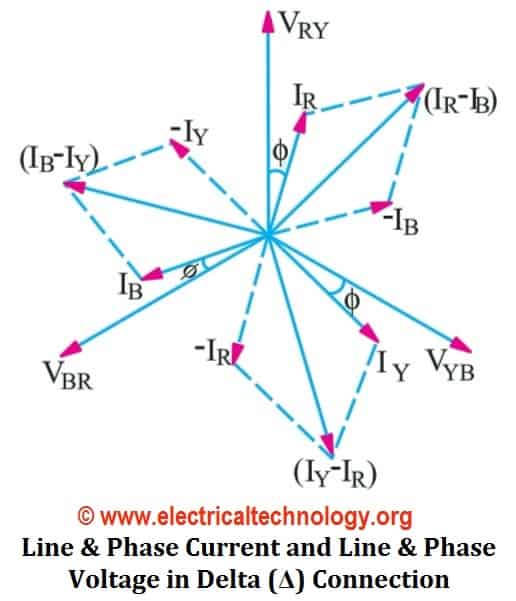
Delta Connection (Δ): 3 Phase Power, Voltage & Current Values — Fig (2). Line & Phase Current and Line & Phase Voltage in Delta (Δ) Connection

The current of Line 1 can be found by determining the vector difference between I_R and I_B and we can do that by increasing the I_B Vector in reverse, so that, I_R and I_B makes a parallelogram. The diagonal of that parallelogram shows the vector difference of I_R and I_B which is equal to current in Line 1= I₁. Moreover, by reversing the vector of I_B, it may indicate as (-I_B), therefore, the angle between I_R and -I_B (I_B, when reversed = -I_B) is 60°. If,

I_R = I_Y = I_B = I_PH …. The phase currents

Then;

The current flowing in Line 1 would be;

I_L or I₁ = 2 x I_PH x Cos (60°/2)

= 2 x I_PH x Cos 30°

= 2 x I_PH x (√3/2) …… Since Cos 30° = √3/2

I_L= √3 I_PH

i.e. In Delta Connection, The Line current is √3 times of Phase Current.

Similarly, we can find the reaming two Line currents as same as above. i.e.,

I₂ = I_Y – I_R … Vector Difference = √3 I_PH

I₃ = I_B – I_Y … Vector difference = √3 I_PH

As, all the Line current are equal in magnitude i.e.

I₁ = I₂ = I₃ = I_L

Hence

IL = √3 I_PH

It is seen from the fig above that;

The Line Currents are 120° apart from each other
Line currents are lagging by 30° from their corresponding Phase Currents
The angle Ф between line currents and respective line voltages is (30°+Ф), i.e. each Line current is lagging by (30°+Ф) from the corresponding line voltage.

Power in Delta Connection

We know that the power of each phase;

Power / Phase = V_{PH x}I_PH x CosФ

And the total power of three phases;

Total Power = P = 3 x V_{PH x}I_PH x CosФ ….. (1)

We know that the values of Phase Current and Phase Voltage in Delta Connection;

I_PH = I_L /√3 ….. (From I_L = √3 I_PH)

V_PH = V_L

Putting these values in power eq……. (1)

P = 3 x V_L x ( I_L/√3) x CosФ …… (I_PH = I_L / /√3)

P = √3 x√3 x V_L x ( I_L/√3) x CosФ …{ 3 = √3x√3 }

P = √3 x V_Lx I_L x CosФ …

Hence proved;

Power in Delta Connection,

P = 3 x V_{PH x}I_PH x CosФ …. or

P = √3 x V_L x I_L x CosФ

Where Cos Φ = Power factor = the phase angle between Phase Voltage and Phase Current (not between Line current and line voltage).

The same is explained in 3-Phase Circuit MCQs with explanatory Answer (MCQs No.1)

Good to Remember:

In both Star and Delta Connections, The total power on balanced load is same.

I.e. total power in a Three Phase System = P = √3 x V_L x I_L x CosФ

Good to know:

Balanced System is a system where:

All three phase voltages are equal in magnitude
All phase voltages are in phase by each other i.e. 360°/3 = 120°
All three phase Currents are equal in magnitude
All phase Currents are in phase by each other i.e. 360°/3 = 120°
A three phase balanced load is a system in which the load connected across three phases are identical.