Norton’s Theorem. Easy Step by Step Procedure with Example

Norton’s Theorem in DC Circuit Analysis

Norton’s theorem is another useful technique to analyze electric circuits like using the Thevenin’s Theorem, which reduces linear, active circuits and complex networks into a simple equivalent circuit. The main difference between Thevenin’s theorem and Norton’s theorem is that, Thevenin’s theorem provides an equivalent voltage source and an equivalent series resistance, while Norton’s theorem provides an equivalent Current source and an equivalent parallel resistance.

Norton’s Theorem states that:

Any linear electric network or complex circuit with current and voltage sources can be replaced by an equivalent circuit containing a single independent current source I_N and a parallel resistance R_N.

In other but simple words, Any linear circuit is equivalent to a real and independent current source in specific terminals.

Related Post: Thevenin’s Theorem. Easy Step by Step Procedure with Example (Pictorial Views)

Steps to Analyze an Electric Circuit using Norton’s Theorem

1. Short the load resistor.
2. Calculate / measure the Short Circuit Current. This is the Norton Current (I_N).
3. Open Current Sources, Short Voltage Sources and Open Load Resistor.
4. Calculate /measure the Open Circuit Resistance. This is the Norton Resistance (R_N).
5. Now, Redraw the circuit with measured short circuit Current (I_N) in Step (2) as Current Source and measured open circuit resistance (R_N) in step (4) as a parallel resistance and connect the load resistor which we had removed in Step (3). This is the Equivalent Norton Circuit of that Linear Electric Network or Complex circuit which had to be simplified and analyzed. You have done it.
6. Now find the Load current flowing through and Load Voltage across Load Resistor by using the Current divider rule. I_L = I_N / (R_N / (R_N+ R_L)) ((For clear explanation … check the solved example given below).

Solved Example by Norton’s Theorem:

Example:

Find R_N, I_N, the current flowing through and Load Voltage across the load resistor in fig (1) by using Norton’s Theorem.

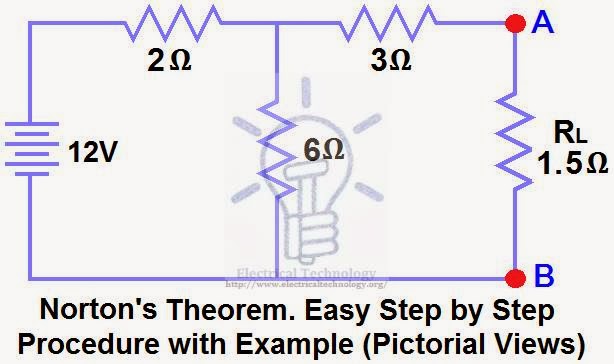
 Solution:-

STEP 1.

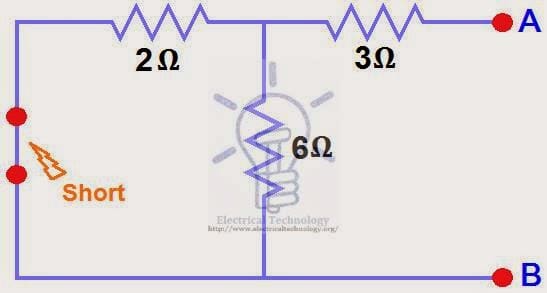
Short the 1.5Ω load resistor as shown in (Fig 2).

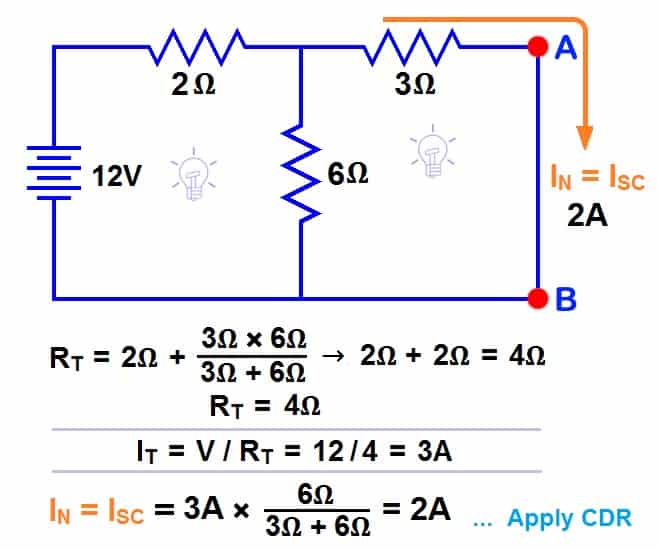
STEP 2.

Calculate / measure the Short Circuit Current. This is the Norton Current (I_N).

We have shorted the AB terminals to determine the Norton current, I_N. The 6Ω and 3Ω are then in parallel and this parallel combination of 6Ω and 3Ω are then in series with 2Ω.

So the total resistance of the circuit to the Source is:-

2Ω + (6Ω || 3Ω) ….. (|| = in parallel with).

R_T = 2Ω + [(3Ω x 6Ω) / (3Ω + 6Ω)] → I_T = 2Ω + 2Ω = 4Ω.

R_T = 4Ω

I_T = V ÷ R_T

I_T = 12V ÷ 4Ω

I_T = 3A..

Now we have to find I_SC = I_N … Apply CDR… (Current Divider Rule)…

I_SC = I_N = 3A x [(6Ω ÷ (3Ω + 6Ω)] = 2A.

I_SC = I_N = 2A.

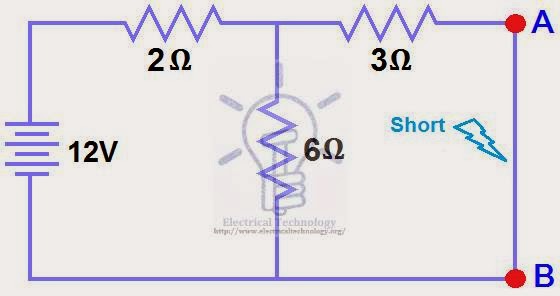
STEP 3.

Open Current Sources, Short Voltage Sources and Open Load Resistor. Fig (4)

STEP 4.

Calculate /measure the Open Circuit Resistance. This is the Norton Resistance (R_N)

We have Reduced the 12V DC source to zero is equivalent to replace it with a short in step (3), as shown in figure (4)  We can see that 3Ω resistor is in series with a parallel combination of 6Ω resistor and  2Ω resistor. i.e.:

3Ω + (6Ω || 2Ω) ….. (|| = in parallel with)

R_N = 3Ω + [(6Ω x 2Ω) ÷ (6Ω + 2Ω)]

R_N = 3Ω + 1.5Ω

R_N = 4.5Ω

STEP 5.

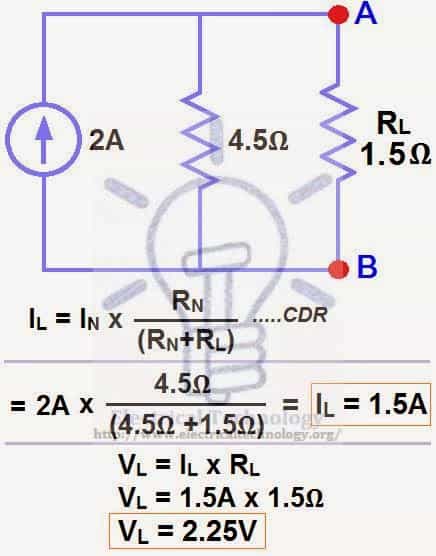
Connect the R_N in Parallel with Current Source I_N and reconnect the load resistor. This is shown in fig (6) i.e. Norton Equivalent circuit with load resistor.

STEP 6.

Now apply the last step i.e. calculate the load current through and Load voltage across the load resistor by Ohm’s Law as shown in fig 7. 

Load Current through Load Resistor…

I_L = I_N x [R_N ÷ (R_N+ R_L)]

= 2A x (4.5Ω ÷ 4.5Ω + 1.5Ω) → = 1.5A

I_L = 1. 5A

And

Load Voltage across Load Resistor…

V_L = I_L x R_L

V_L = 1.5A x 1.5Ω

V_L= 2.25V

Now compare this simple circuit with the original circuit given in figure 1. Can you see how much easier it will be to measure/calculate the load current and load Voltage for different load resistors through Norton’s Theorem even in much more complex circuits? Only and only yes.

Good to know: Both Norton’s & Thevenin’s theorems can be applied to both AC and DC circuits containing difference components such as resistors, inductors and capacitors etc. Keep in mind that the Norton’s current “I_N” in AC circuit is expressed in complex number (polar form) whereas, the Norton’s resistance “R_N” is stated in rectangular form.

Related Posts:

• Maximum Power Transfer Theorem for AC & DC Circuits
• Kirchhoff’s Current & Voltage Law (KCL & KVL) | Solved Example
• Compensation Theorem – Proof, Explanation and Solved Examples
• Substitution Theorem – Step by Step Guide with Solved Example
• Millman’s Theorem – Analyzing AC & DC Circuits – Examples
• Superposition Theorem – Circuit Analysis with Solved Example
• Tellegen’s Theorem – Solved Examples & MATLAB Simulation
• SUPERNODE Circuit Analysis | Step by Step with Solved Example
• SUPERMESH Circuit Analysis | Step by Step with Solved Example
• Voltage Divider Rule (VDR) – Solved Examples for R, L and C Circuits
• Current Divider Rule (CDR) – Solved Examples for AC and DC Circuits
• Star to Delta & Delta to Star Conversion. Y-Δ Transformation